Track Map
(Dernière mise à jour : Version 1.4 - Août 2024)
Voici une petite application sympa destinée à tracer des plans simples, par exemple dans le cadre de la conception d'un réseau de modélisme ferroviaire.
Le principe est simple : il suffit de fournir
- les coordonnées d'un point de départ
- un rayon et un angle
- la longueur d'un trait
Les données doivent être préalablement enregistrées dans un fichier au format texte appelé "track_data.txt".

Exemple de « track_data.txt »
1000 * 500 # Dimensions du plan
100, 50, 0 # Coordonnées du point de départ
100 # ligne horizontale de longueur 100
200, 30 # courbe de 30° vers le haut, rayon 200
115.47 # ligne droite de longueur 115.47
300, 15 # nouvelle courbe de 15°
200 # ligne droite
150, -45 # repasser à l'horizontale
150 # ligne droite
462.1 , 182.2 , 45 # se repositionner au début de "l'aiguillage"
100, 30 # aiguillage 30° vers la gauche
200 # ligne droite
La première ligne du fichier doit comporter deux nombres séparés par * : il s'agit des dimensions du plan (par exemple 1000 * 500, en millimètres)
Les nombres décimaux doivent utiliser le point et non pas la virgule.
Les virgules servent à séparer les nombres en suivant la syntaxe expliquée plus loin.
Résultat

La syntaxe est la suivante :
- une ligne vide signifie afficher les coordonnées du point
-
color permet de choisir la couleur (ajouté dans la v. 1.1 - jan. 2023) ; exemple : color red
voir https://matplotlib.org/stable/gallery/color/named_colors.html pour les choix de couleurs - trois nombres x, y et a, séparés par une virgule, signifient se placer aux coordonnées (x, y) et afficher la suite en suivant la direction donnée par l'angle "a" (voir note plus bas)
- un nombre n signifie : tracer une ligne droite de longueur n au départ du dernier point connu
- deux nombres r et a séparés par une virgule signifient tracer une courbe de rayon r et d'angle a
- les commentaires éventuels peuvent être ajoutés derrière le caractère #
- radius off (et radius on) permet de désactiver (et de réactiver) l'affichage des rayons de courbure (option ajoutée dans la v. 1.4 - août 2024)
Note :
- si a vaut zéro : direction horizontale vers la droite du plan
- si a est positif : direction dans le sens "trigonométrique"
- si a est négatif : direction dans le sens "horlogique"
Code Python
# Track_Map.py
#
# Copyright (C) 2022-2023 PhS & Quintilien
#
# This program is free software; you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation; either version 2 of the License, or
# (at your option) any later version.
# This program is distributed in the hope that it will be useful,
# but WITHOUT ANY WARRANTY; without even the implied warranty of
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
# See the GNU General Public License for more details.
#
# Current rev. 1.4 (aug 2024) : radius on/off
#
# Previous rev.
# 1.0 (dec. 2022)
# 1.1 (jan 2023) : color selection
# 1.3 (jan 2023) : error message when "track_data.txt" not found
# 1.4 (aug 2024) : radius on/off
import matplotlib.pyplot as plt
import numpy as np
from numpy import sin, cos, pi, linspace
filename = "track_data.txt"
fontsz = 7
plotsz = 10
plotcol = 'blue'
rad_flag = True
#
# Syntaxe du contenu du fichier
# ligne vide : afficher les coordonnées
# 1 élément : longueur d'une droite (ou sélection de la couleur àpd v. 1.1)
# 2 éléments : rayon de courbure, angle
# 3 : positionner aux coordonnées x, y avec une direction donnée
# color ... : sélectionner une couleur
# radius ... : off pour désactiver l'affichage des valeurs des rayons ; on pour réactiver
#
plt.text(5, -150, 'Track_map v. 1.4', color='grey', fontsize=5)
fi = ''
try:
with open(filename, "r") as f:
fi = f.read()
f.close()
except:
plt.text(150, 220, 'File not found : "'+filename+'"', color='red', fontsize=15)
x1 = 0
y1 = 0
a1 = 0
def coord(x, y, a): # afficher coordonnées
# paramètres : coordonnées, angle de départ, direction (angle)
plt.plot([x,x,0] , [0,y,y], '--', color = 'black', linewidth=0.5)
plt.scatter(x,y,s=8,c='red')
if x not in x_displ:
x_displ.append(x)
if y not in y_displ:
y_displ.append(y)
def lin(x, y, a, lg): # tracer une ligne droite
# coordonnées, angle de départ, longueur
x1 = x + ( lg * cos( a / 180 * pi ) )
y1 = y + ( lg * sin( a / 180 * pi ) )
plt.plot( [ x , x1 ] , [ y , y1 ] , color = plotcol, linewidth=2)
plt.scatter(x1,y1,s=plotsz,c=plotcol)
# retourne les coordonnées finales et la direction finale (l'angle)
return x1, y1, a
def arc(x, y, a, r, c): # tracer un arc de cercle
# coordonnées, angle de départ, rayon, courbure
k = 'green'
if abs(c) == 7.5:
k = 'red'
if abs(c) == 15:
k = 'magenta'
if abs(c) == 90 or abs(c) == 180 :
k = 'black'
# calcul des coordonnées du centre du rayon de courbure
if c >=0 :
x_ctr = x - ( r * sin( a / 180 * pi ) )
y_ctr = y + ( r * cos( a / 180 * pi ) )
else:
x_ctr = x + ( r * sin( a / 180 * pi ) )
y_ctr = y - ( r * cos( a / 180 * pi ) )
# coordonnées du dernier point de l'arc
# (le premier point est connu : x, y)
if c >=0 :
x2 = x_ctr + r * sin ( ( a + c ) / 180 * pi )
y2 = y_ctr - r * cos ( ( a + c ) / 180 * pi )
else:
x2 = x_ctr - r * sin ( ( a + c ) / 180 * pi )
y2 = y_ctr + r * cos ( ( a + c ) / 180 * pi )
# calcul de l'arc ( = série d'angles)
if c >=0 :
angles = linspace( ( -90 + a ) / 180 * pi, ( -90 + a + c ) / 180 * pi, 100 )
else:
angles = linspace( ( 90 + a ) / 180 * pi, ( 90 + a + c ) / 180 * pi, 100 )
# texte indication courbure (on n'affiche pas les angles de 180° car ils sont évidents)
if abs(c) != 180:
if c >=0 :
x_txt = x_ctr + ( r/2 * cos( ( a + c/2 - 90 ) / 180 * pi ) ) - 1.0
y_txt = y_ctr + ( r/2 * sin( ( a + c/2 - 90 ) / 180 * pi ) ) - 0.01
else :
x_txt = x_ctr + ( r/2 * cos( ( a + c/2 + 90 ) / 180 * pi ) ) - 1.0
y_txt = y_ctr + ( r/2 * sin( ( a + c/2 + 90 ) / 180 * pi ) ) - 0.01
if rad_flag: # v; 1.4 (aug. 2024)
plt.text( x_txt , y_txt , str(c)+'°', color = k , fontsize = fontsz)
xs = r * cos(angles) + x_ctr
ys = r * sin(angles) + y_ctr
if rad_flag: # v; 1.4 (aug. 2024)
# tracer le centre
plt.plot([x_ctr,x],[y_ctr,y], '--', color = k, linewidth=0.5)
plt.scatter(x_ctr,y_ctr,s=3,c='green')
# tracer point d'arrivée
plt.scatter(x2,y2,s=plotsz,c=plotcol)
# tracer rayon final
if rad_flag: # v; 1.4 (aug. 2024)
plt.plot([x_ctr,x2],[y_ctr,y2],
'--', color = k, linewidth=0.5)
# tracer l'arc
plt.plot(xs, ys, color = plotcol, linewidth=2)
x = xs[-1]
y = ys[-1]
a = a + c
# retourne les coordonnées finales et la direction finale (l'angle)
return x, y, a
# dimensions du plan par défaut
x_max = 1000.0
y_max = 500.0
# affichage des coordonnées sur les axes
x_displ = list()
y_displ = list()
# lecture du fichier
for n, rec in enumerate (fi.split("\n")):
lg = 0
ra = 0
cr = 0
rec = rec.strip()
rec = rec.split("#") # ce qui suit un caractère # éventuel
# est considéré comme un commentaire
rec = rec[0]
rec = rec.split("*") # s'il y a un '*' : interprêter comme
# les dimensions max. de x et y
if len(rec) > 1:
try:
x_max = float(rec[0].strip())
y_max = float(rec[1].strip())
except:
pass
print (x_max, y_max)
else:
rec = rec[0]
if rec == '': # ligne vide : afficher les coordonnées et
coord(x1, y1, a1) # la direction (l'angle) de départ
else:
li =rec.split(",")
if len(li) == 1: # 1 élément
if li[0].lower().find('color') != -1: # v.1.1 (jan 2023)
plotcol = li[0].replace('color','').lower().strip()
elif li[0].lower().find('radius') != -1: # v.1.4 (aug 2024)
if li[0].lower().find('off') != -1:
rad_flag = False
else:
rad_flag = True
else: # 1 élément : longueur d'une droite
try:
lg = float(li[0].strip())
x1,y1,a1 = lin(x1,y1,a1,lg)
except:
pass
if len(li) == 2: # 2 éléments : rayon de courbure, angle
try:
ra = float(li[0].strip())
cr = float(li[1].strip())
x1, y1, a1 = arc(x1, y1, a1, ra, cr) # coordonnées,
# angle de départ,
# rayon, courbure
except:
pass
if len(li) == 3: # 3 éléments : positionner aux coordonnées
# x, y avec une direction donnée
try:
x1 = float(li[0].strip())
y1 = float(li[1].strip())
a1 = float(li[2].strip())
x1,y1,a1 = lin(x1,y1,a1,0)
except:
pass
plt.xlim(0, x_max)
plt.ylim(0, y_max)
plt.gca().set_aspect('equal')
# affichage des coordonnées sur les axes
x_displ.append(x_max)
y_displ.append(y_max)
plt.xticks(x_displ, fontsize = 'xx-small')
plt.yticks(y_displ, fontsize = 'xx-small')
plt.show()
print ('*** End ***')
Track_map « .exe » (Windows)
L'exécution du code repris ci-dessus nécessite l'installation préalable
- du langage Python
- des bibliothèques numpy et matplotlib
Pour ceux qui souhaitent se simplifier la vie, il est également possible de télécharger ici une version directement exécutable sous Windows.
Le fichier zip téléchargé doit être décompressé.
Ce fichier contient les bibliothèques, les DLLs, l'exécutable (track_map.exe) ainsi qu'un exemple de track_data.txt
En procédant de la sorte, il n'est pas nécessaire d'installer Python.
Application pratique : le modélisme ferroviaire
Géométrie de la voie Fleischmann « Piccolo », à l'échelle « N » (échelle 1/160ème)

Fichier « track_data.txt » pour entre axes 33.6 mm
400 * 200 # Dimensions du plan
0, 100, 0 # point d'origine
111 # partie rectiligne de l'aiguillage
111 # rail droit ref Fleischmann 9101
0, 100, 0 # point d'origine
303 , 15 # courbe aiguillage (gauche)
33.45 # fin courbe aiguillage (prolongation rectiligne théorique)
430 , -15 # contre-courbe
Résultat obtenu

Autres entre axes

Fichier « track_data.txt » pour entre axes 48 mm
400 * 200 # Dimensions du plan
0, 100, 0 # point d'origine
111 # partie rectiligne de l'aiguillage
color red
55.5 # ref Fleischmann 9103
color blue
111 # rail droit ref Fleischmann 9101
0, 100, 0 # point d'origine
303 , 15 # courbe aiguillage (gauche)
33.45 # fin courbe aiguillage (prolongation rectiligne théorique)
color green
57.5 # ref Fleischmann 9102
color blue
430 , -15 # contre-courbe
Résultat obtenu

Fichier « track_data.txt » pour entre axes 63 mm
400 * 200 # Dimensions du plan
0, 100, 0 # point d'origine
111 # partie rectiligne de l'aiguillage
color red
111 # rail droit ref Fleischmann 9101
color blue
111 # rail droit ref Fleischmann 9101
0, 100, 0 # point d'origine
303 , 15 # courbe aiguillage (gauche)
33.45 # fin courbe aiguillage (prolongation rectiligne théorique)
color green
57.5 # ref Fleischmann 9102
color red
57.5 # ref Fleischmann 9102
color blue
430 , -15 # contre-courbe
Résultat obtenu

Rayons de courbure

Fichier « track_data.txt » pour aiguillage courbe
400 * 350 # Dimensions du plan
0, 100, 0 # point d'origine
192 , 45 # courbe intérieure de l'aiguillage (= R1, 45°)
color green
192 , 45 # prolongement de la courbe intér. par ref Fleischmann 9120
color blue
0, 100, 0 # retour au point d'origine
33.6 # portion rectiligne théorique courbe extérieure de l'aiguillage
192 , 45 # portion courbe de l'aiguillage vers l'extérieur
color green
192 , 45 # prolongement de la courbe intér. par ref Fleischmann 9120
Résultat obtenu

Références Fleischmann utilisées

Exemple de circuit Fleischmann
Cet exemple correspond au contenu des coffrets de départ B1 - 919010 et C1 - 919011

Fichier « track_data.txt »
1200 * 500 # https://www.fleischmann.de/ffr/produits/rails/n-rails-avec-lit/coffrets-de-rails/919011-coffret-de-voies-c1.html
210, 60, 0 # point d'origine en bas à gauche
color red
111 # portion droite de l'aiguillage en bas à gauche
111
color blue
222
222
111
192, 45
color red
192, 45
color blue
192, 45
192, 45
111
222
222
222
192, 45
192, 45
192, 45
192, 45
210, 60, 0 # point d'origine en bas à gauche
color red
303 , -15 # courbe aiguillage (droite)
33.45 # fin courbe aiguillage (prolongation rectiligne théorique)
430 , 15 # contre-courbe réf 9136
color blue
222
color red
222
111
color blue
192, 45
1179, 252, -90 # début aiguillage courbe
color red
33.6 # portion rectiligne théorique courbe extérieure de l'aiguillage
192 , -45 # portion courbe de l'aoguillage vers l'extérieur
color blue
987, 444, -180
303 , 15 # courbe aiguillage (gauche)
33.45 # fin courbe aiguillage (prolongation rectiligne théorique)
color red
111 # rail de découplement réf 9114
color blue
220
220
57.5 # rail avec heurtoir
Résultat obtenu
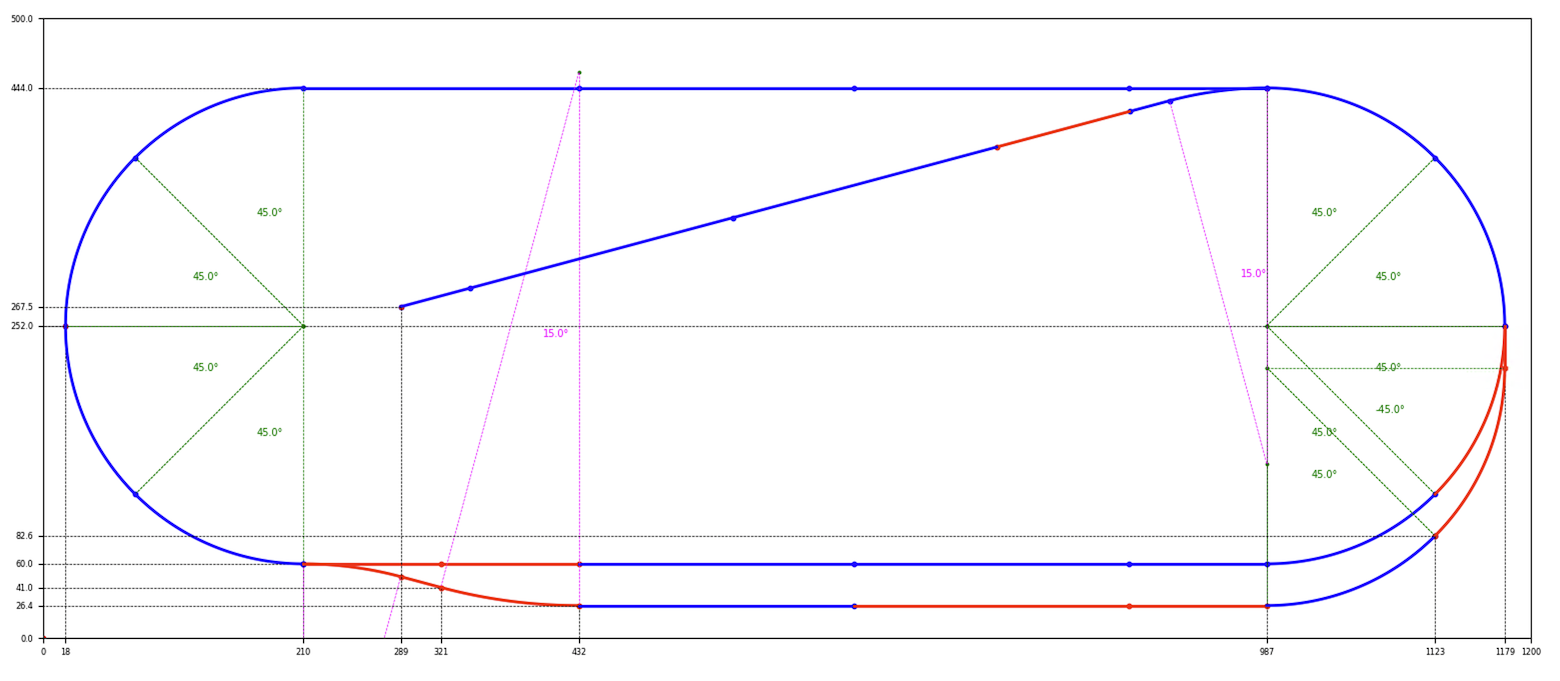
Schéma proposé par Fleischmann

Pour les matheux ...
L'application se base sur les calculs suivants

(Croquis réalisés « à la main » sur un iPad au moyen de l'application Nebo !)